
Round: 217
In the following diagram, each blue line is 24 centimetres long, and the red line is 16 centimetres long. Assume the shape in the centre of the circle is a perfect square, and it is exactly centred in the circle. Also assume that all three coloured lines are parallel to each other.

What is the radius of the circle, in centimetres? Please round up to the nearest centimetre.
Answer: 26 centimetres
Here's how to solve it:
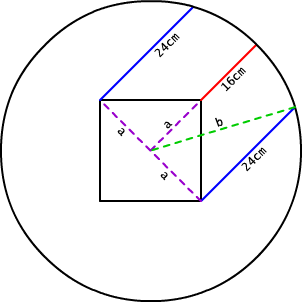
The radius is equal to the length of any line that goes from the center of the circle to the edge. In this diagram, we see that there are two lines that do that: the red line plus the purple dotted line (16 + a) and the green dotted line (b).
Using the Pythagorean theorem, we know that b2 = a2 + 242. We also know that b is the radius, so we can substitute 16 + a for b. So, we get:
(a + 16)2 = a2 + 242
Doing some of the algebra:
a2 + 32a + 162 = a2 + 242
Take out the a2 from both sides and do the math:
32a + 256 = 576
32a = 320
a = 10
And as we found earlier, the radius is 16 + a, so we get our answer of 16 + 10 = 26!
Close window